Boîte ailée
Boîtes simples
Pyramide droite à base carrée
Pyramide tronquée droite à base carrée
ou boîte traditionnelle japonaise
Pyramide tronquée droite à base carrée
ORIGAMIS
ET
MATHEMATIQUES
Problèmes à composer
cliquer
sur les photos
|
Boîte ailée |
|
Boîtes simples |
|
Pyramide droite à base carrée |
|
Pyramide tronquée droite à base carrée ou boîte traditionnelle japonaise |
|
Pyramide tronquée droite à base carrée |
|
Boîte cubique |
|
Pyramide droite à base triangulaire |
|
Tétraèdre régulier |
|
Shuriken ou étoile Ninja |
Vidéogrammes
montrant ces pliages et d'autres en caméra
subjective disponibles sur www.origamis.c.la
 |
But :
trouver la valeur de x pour que la boîte ait une
capacité de a ml ou a cm³ Prérequis : calcul dans R, volume d’un cube, d’un parallélépipède rectangle Découverte : racine cubique d’un réel |
Réponse :
Schéma :
|
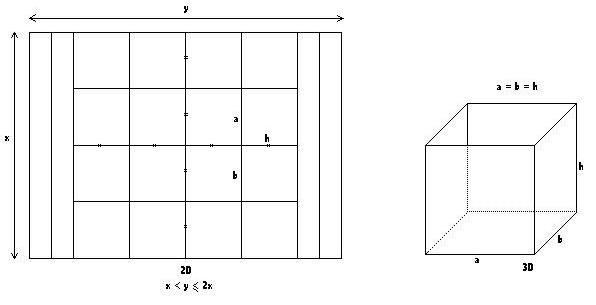
But : calculer les largeurs x2 et x3 des feuillets permettant de fabriquer deux compartiments 1/3 2/3 emboîtables dans la grande boîte
Prérequis : calcul dans R, équations du 1er degré à une inconnue réelle, transformation d’expressions simples
Réponse : si pour la grande boîte, on part d’une feuille rectangulaire mesurant x1 = 21cm et y = 29,7 cm, alors x2 = 18,4 cm et x3 = 13,6 cm
Schéma :
 |
But :
calculer le volume V de la pyramide en fonction de la
longueur x du côté du feuillet carré permettant le
pliage Prérequis : calcul dans R, trigonométrie des triangles rectangles, volume d’une pyramide, isométrie des triangles, théorème de Pythagore, calcul sur les radicaux |
Réponse :
où a = 22°30’
Schéma :
PYRAMIDE TRONQUEE OU BOITE TRADITIONNELLE JAPONAISE
|
But :
calculer le volume V de la pyramide en fonction de la
longueur x du côté du feuillet carré permettant le
pliage Prérequis : calcul dans R, trigonométrie des triangles rectangles, volume d’une pyramide, isométrie des triangles, théorème de Pythagore, calcul sur les radicaux, similitude des triangles, règles des proportions |
Réponse :
V = k’ x3 avec
Schéma :
 |
But :
calculer le volume V de la pyramide en fonction de la
longueur x du côté du feuillet carré permettant le
pliage Prérequis : calcul dans R, trigonométrie des triangles rectangles, volume d’une pyramide, isométrie des triangles, théorème de Pythagore, calcul sur les radicaux, similitude des triangles, règles des proportions |
Réponse :
V = k’ x3 avec
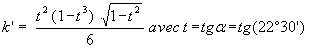
Schéma :
|
But : trouver
la valeur de x (largeur de la feuille rectangulaire) pour que la boîte ait une capacité de a ml ou a cm³ Prérequis : calcul
dans R, volume d’un cube, |
Réponse :
Schéma :
RETOUR
AU DEBUT
PYRAMIDE DROITE A BASE TRIANGULAIRE
|
But : trouver
le volume de la pyramide en connaissant la longueur x du
côté du feuillet permettant le pliage Prérequis : calcul dans R, racines carrées: calcul et simplification, trigonométrie du triangle rectangle, volume d'une pyramide, théorème de Pythagore |
Réponse :
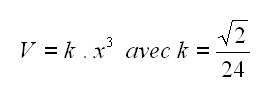
Schéma :
En assemblant 4 de ces pyramides, on obtient un cube dont la
partie inoccupée à l'intérieur
est un tétraèdre régulier. La somme des volumes de ces 5
solides peut être calculée, elle
doit correspondre au volume du cube.
Lien vidéo n°1
 |
On peut demander de
calculer le volume en fonction de l'arête, on peut aussi
demander de calculer l'arête, puis le volume en
connaissant les dimensions de la feuille de départ (A4)
ou imposer une longueur d'arête et demander les
dimensions de la feuille... Prérequis : calcul dans R, racines carrées: calcul et simplification, trigonométrie du triangle rectangle ou les similitudes et proportions, volume d'une pyramide, théorème de Pythagore |
|
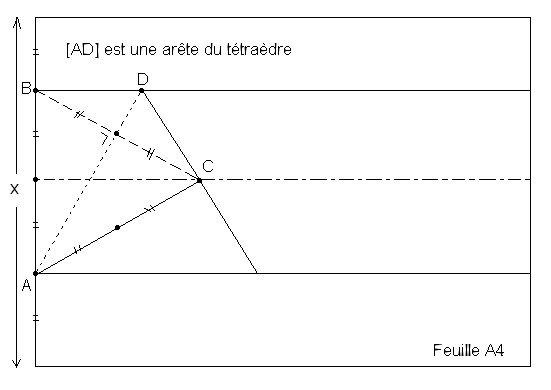
On peut demander de
calculer la distance entre deux pointes en fonction des
dimensions de la feuille ou l'inverse Prérequis : théorème de Pythagore, calcul dans R, racines carrées: calcul et simplification, similitudes et proportions, |
publié en mars 2008 - dernière mise à jour décembre 2012- nuagerouge@gmail.com - www.maths.c.la - www.gis.c.la - www.origamis.c.la
